Converting 2D Architectural Drawings into Hierarchical Scene Graph Representations

In this ongoing research, we outline a theoretical framework for transforming architectural 2D drawings into hierarchical scene graph representations. Traditional floorplans carry far more than rectangular outlines: they contain rich spatial relationships, complex room shapes, and functional constraints. Our approach bridges graph-theoretic floorplan analysis, hierarchical scene modeling, and constraint reasoning to produce robust, semantically enriched representations suitable for advanced constrained architectural planning.

Background and Motivation

Graph-Theoretic Floorplan Analysis

Many architectural drawings can be naturally modeled as planar graphs, where:

• Nodes represent rooms or spatial units.
• Edges capture adjacency relationships, such as shared walls, doors, or corridors.

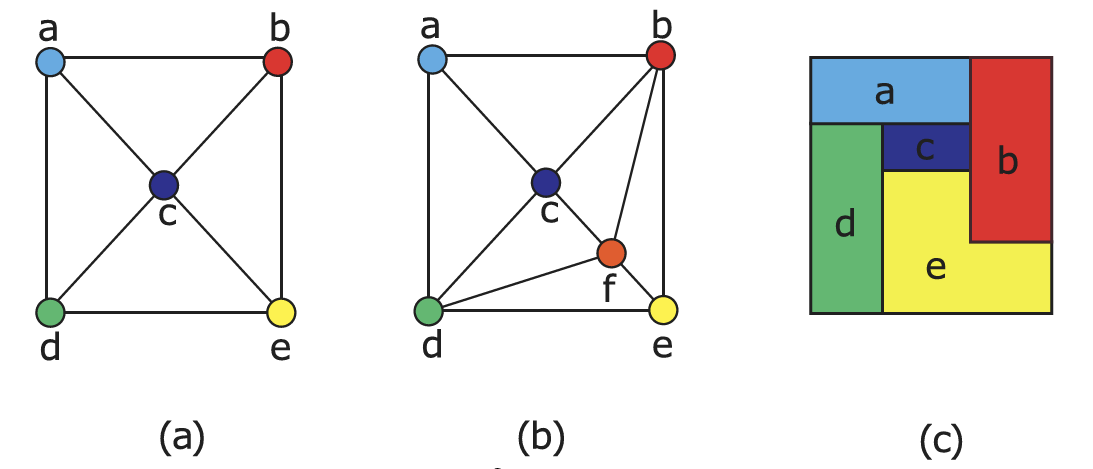
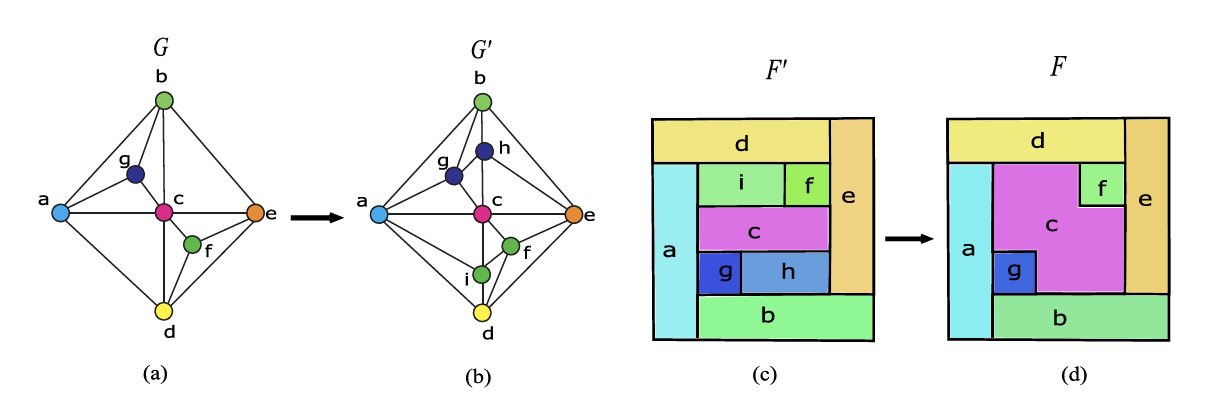
However, real-world floorplans often include non-rectangular rooms (e.g., L-, T-, F-, cross-shaped, or multigonal-shaped), which complicate pure rectangular decompositions. As identified in various graph-theoretic models, separating triangles (cycles of three nodes) indicate an impossibility for strictly rectangular tiling. By strategically splitting edges and introducing auxiliary vertices, one can expand such triangles into quadrilaterals or higher-order polygons, thus enabling a more flexible and accurate representation of non-rectangular spaces.

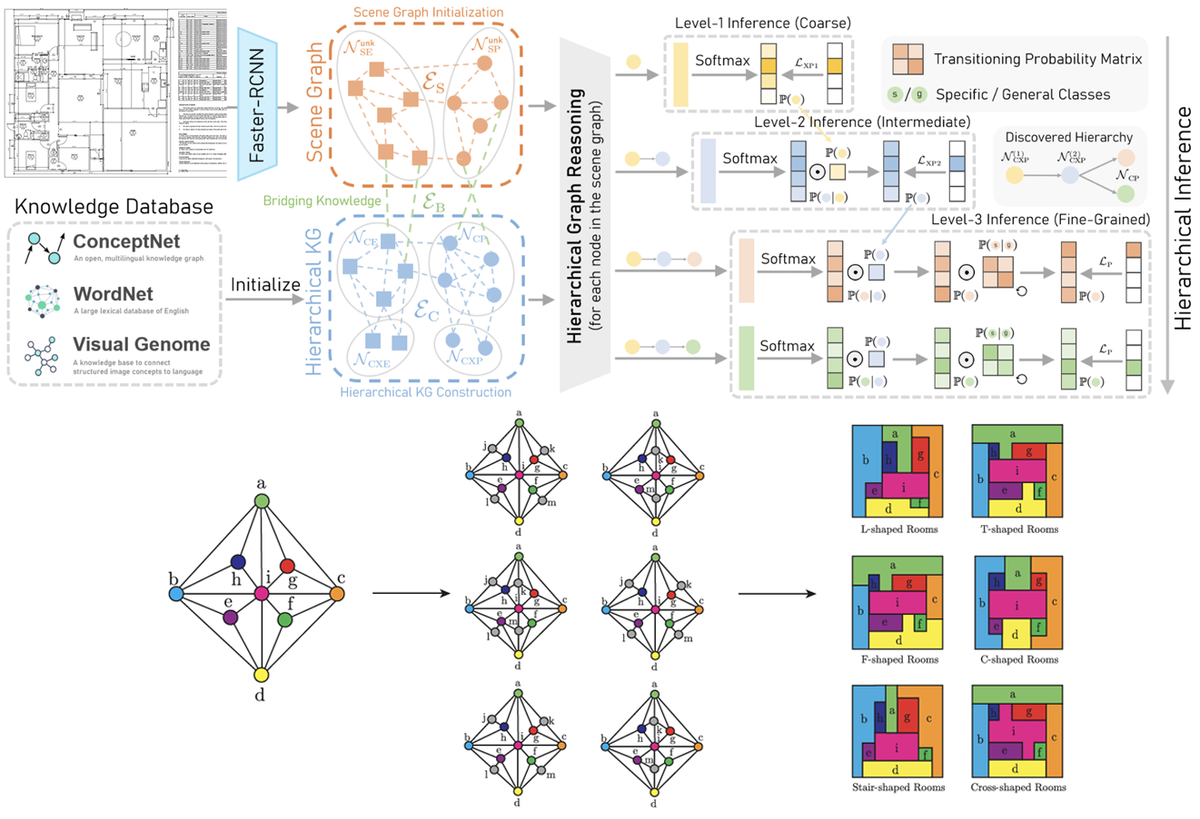
Hierarchical Scene Graph Models

Scene graphs represent the semantic and structural relationships in a visual scene. In an architectural context, this means:

1. Global Level: A top-level scene graph capturing each room’s geometric and topological properties.
2. Local Level: Within each room, a subgraph details interior objects, furniture, and fine-grained features.

This two-tiered approach (coarse-to-fine inference) draws on hierarchical knowledge representations (akin to approaches like HiKER-SGG), where we first identify broad categories (e.g., “Room” vs. “Corridor,” or “Furniture” vs. “Appliance”) and then refine these into more specific labels.

Constraint Reasoning in Indoor Spaces

Indoor spatial modeling often requires satisfying multiple constraints:

• Adjacency: Rooms sharing walls or doorways must remain consistently connected in any representation.
• Dimensional: Minimum or maximum room sizes, aspect ratios, and other geometric properties must hold true.
• Pathway: Distances or travel times between certain areas must not exceed specified thresholds.

By embedding these constraints into a constraint solver framework, we can ensure that the final scene graphs are both topologically accurate and functionally viable.

Theoretical Framework

Our pipeline integrates three pillars: graph transformations, hierarchical scene graph construction, and constraint-based validation, to move from a raw 2D architectural layout to a machine-interpretable scene graph.

1. Preprocessing & Structural Extraction

1. Boundary Extraction: We extract the walls, doors, and polygonal outlines from the 2D drawing.
2. Graph Construction: Each identified room or spatial area becomes a node, and adjacency lines become edges, forming a planar graph ( G(V, E) ).

2. Floorplan Graph Generation & Non-Rectangular Room Handling

1. Detecting Separating Triangles

• Cycles of length three \( (v_i \to v_j \to v_k \to v_i) \) signal that a purely rectangular layout may be infeasible.

2. Edge Splitting & Auxiliary Vertices

• To accommodate non-rectangular shapes, we split edges in these cycles, introducing auxiliary vertices that allow higher-order polygons to emerge (e.g., from triangle to quadrilateral).

3. Graph Merging & Table Representation

• We adopt a merging strategy inspired by HiKER-SGG to integrate the adjusted polygons back into the global floorplan.
• In parallel, an abstract table tracks each room’s properties: shape type (L, T, F, multigonal etc.), area, perimeter, and boundary coordinates. This dual approach (graph + table) makes it straightforward to filter or select floorplans with specific geometric criteria.

3. Hierarchical Scene Graph Construction

1. Global Graph (Floorplan-Level)

• Every room node from the floorplan is incorporated into a high-level scene graph.
• Spatial adjacencies between rooms become edges, maintaining the overall layout structure.

2. Local Subgraph (Interior-Level)

• Inside each room, subgraphs represent furniture, fixtures, and other interior details.
• A coarse-to-fine classification strategy is used, starting with broad categories (e.g., “furniture”) and refining to more specific items (e.g., “table,” “sofa,” “desk”).

3. Bridge Edges

• We link local subgraphs back to their corresponding global room nodes. This ensures a unified, hierarchical scene graph that captures both the macro (room-level) and micro (object-level) semantics.

4. Constraint Formulation & Solving

1. Constraint Equations

• Adjacency constraints ensure that if two rooms share a boundary in the drawing, their corresponding nodes remain connected.
• Dimensional constraints enforce permissible room sizes or shape ratios (e.g., \( \text{area}_{\text{room}} \geq \alpha \) ).
• Pathway constraints set maximum allowable distances or path lengths between key areas (e.g., from a living room to an exit), from the "indoor" topological space.

2. Iterative Refinement

• We embed these constraints into a constraint satisfaction model.
• The scene graph is iteratively adjusted until all constraints are satisfied, ensuring fidelity to both the original 2D layout and the user’s functional requirements (like egress or adjacency rules).

Discussion and Ongoing Work

Our theoretical framework fuses insights from:

• Graph Theory: Addressing non-rectangular room shapes via separating triangle detection and edge splitting.
• Hierarchical Models: Using scene graph structures to capture the layered nature of rooms and their interior objects.
• Constraint Optimization: Ensuring the final representation respects real-world requirements (dimensions, connectivity, etc.).

Ongoing research focuses on improving the robustness of the informed merging process, especially for highly complex floorplans, and extending the local subgraph inference to handle nuanced interior details (e.g., subcategories of furniture or specialized architectural features). Additionally, we are exploring how to automate the assignment of shape types based on geometric heuristics and coordinate patterns.

Conclusion

In this work, we offer a multi-stage theoretical framework for converting architectural 2D drawings into hierarchical scene graph representations. By integrating planar graph transformations for non-rectangular room configurations, hierarchical (coarse-to-fine) models for room and object classification, and constraint-based reasoning for functional viability, our approach provides a comprehensive pipeline suitable for advanced indoor spatial analysis and architectural design.